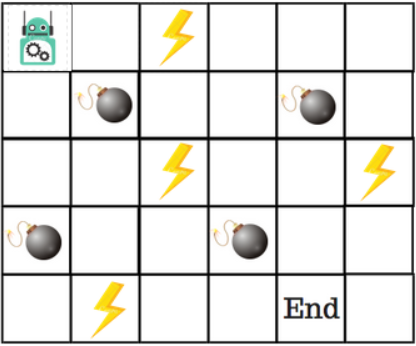
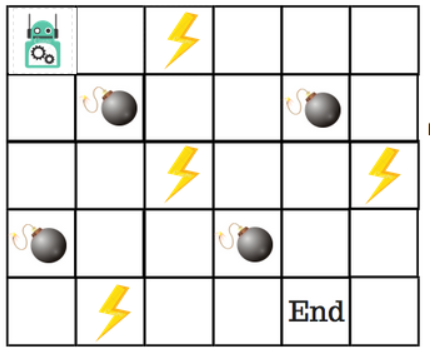
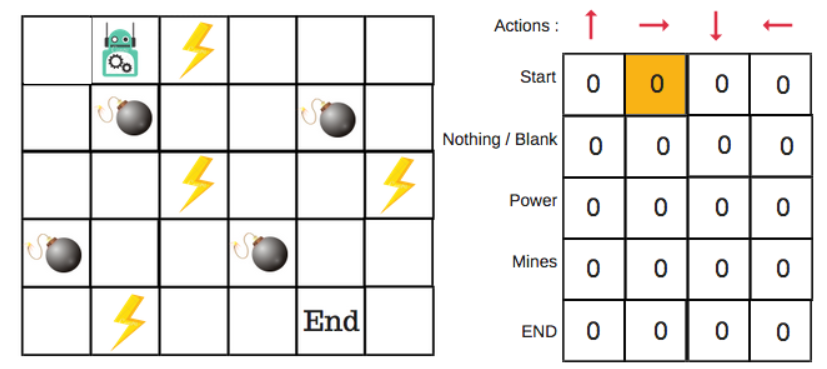
Let’s say that a robot has to cross a maze and reach the end point. There are mines, and the robot can only move one tile at a time. If the robot steps onto a mine, the robot is dead. The robot has to reach the end point in the shortest time possible.
The scoring/reward system is as below:
1. The robot loses 1 point at each step. This is done so that the robot takes the shortest path and reaches the goal as fast as possible.
2. If the robot steps on a mine, the point loss is 100 and the game ends.
3. If the robot gets power ⚡️, it gains 1 point.
4. If the robot reaches the end goal, the robot gets 100 points.
Now, the obvious question is: How do we train a robot to reach the end goal with the shortest path without stepping on a mine?
Q-Table is just a fancy name for a simple lookup table where we calculate the maximum expected future rewards for action at each state. Basically, this table will guide us to the best action at each state.
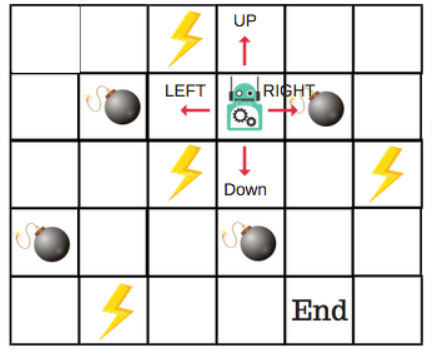
There will be four numbers of actions at each non-edge tile. When a robot is at a state it can either move up or down or right or left.
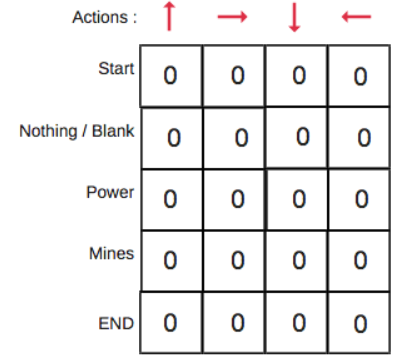
So, let’s model this environment in our Q-Table.
In the Q-Table, the columns are the actions and the rows are the states.
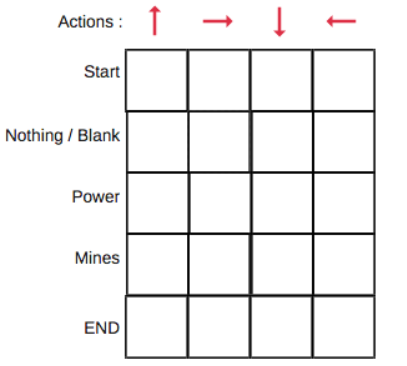
Each Q-table score will be the maximum expected future reward that the robot will get if it takes that action at that state. This is an iterative process, as we need to improve the Q-Table at each iteration.
The Q-function uses the Bellman equation and takes two inputs: state (s) and action (a).
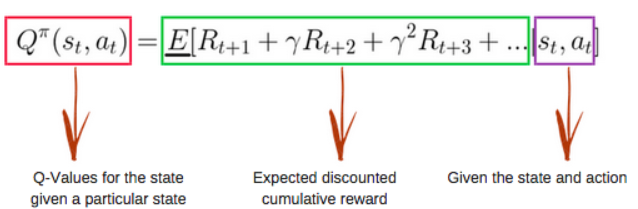
Using the above function, we get the values of Q for the cells in the table.
When we start, all the values in the Q-table are zeros.
There is an iterative process of updating the values. As we start to explore the environment, the Q-function gives us better and better approximations by continuously updating the Q-values in the table.
Now, let’s understand how the updating takes place.
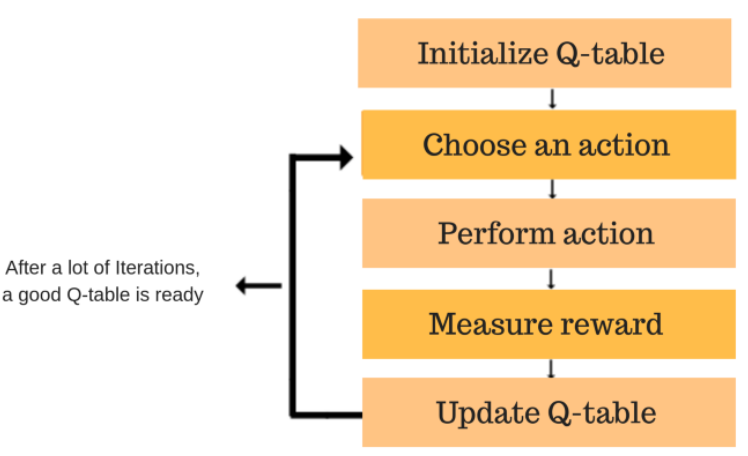
Each of the colored boxes is one step. Let’s understand each of these steps in detail.
We will first build a Q-table. There are n columns, where n= number of actions. There are m rows, where m= number of states. We will initialise the values at 0.
This combination of steps is done for an undefined amount of time. This means that this step runs until the time we stop the training, or the training loop stops as defined in the code.
We will choose an action (a) in the state (s) based on the Q-Table. But, as mentioned earlier, when the episode initially starts, every Q-value is 0.
So now the concept of exploration and exploitation trade-off comes into play. This article has more details.
We’ll use something called the epsilon greedy strategy.
In the beginning, the epsilon rates will be higher. The robot will explore the environment and randomly choose actions. The logic behind this is that the robot does not know anything about the environment.
As the robot explores the environment, the epsilon rate decreases and the robot starts to exploit the environment.
During the process of exploration, the robot progressively becomes more confident in estimating the Q-values.
For the robot example, there are four actions to choose from: up, down, left, and right. We are starting the training now — our robot knows nothing about the environment. So the robot chooses a random action, say right.
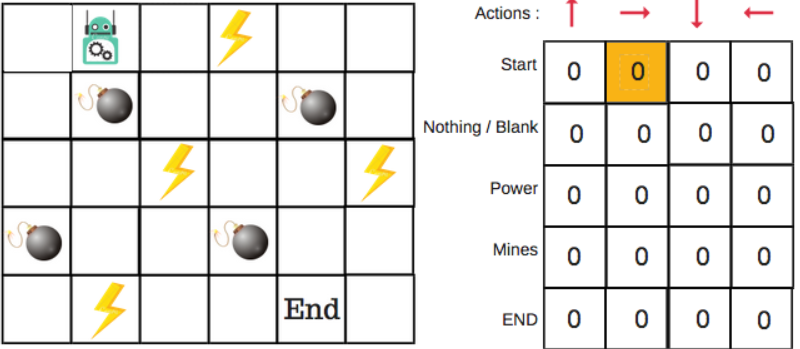
We can now update the Q-values for being at the start and moving right using the Bellman equation.
Now we have taken an action and observed an outcome and reward.We need to update the function Q(s,a).

In the case of the robot game, to reiterate the scoring/reward structure is:
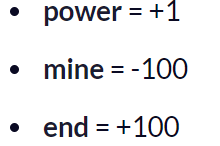

We will repeat this again and again until the learning is stopped. In this way the Q-Table will be updated.
Implement a Q-Learning Java library according to the following requirements.
1. Define an interface RLable which declares the following functions.
// sample code
public interface RLable {
void init(); // init program
void process(); // RL processing
double maxQ(int s); // find out the max Q
public int policy(int state); // base policy to goto next state
double Q(int s, int a); // return Q table value
void setQ(int s, int a, double value); // set Q table
int R(int s, int a); // reward
void printResult(); // Q table
void showPolicy(); // show each steps
}
2. Create a class to implement the interface.
// sample code
public class RLExample implements RLable{
final DecimalFormat df = new DecimalFormat("#.##");
double alpha = 0.1;
double gamma = 0.9;
int episodes = 500; // max episodes
int statesCount = 0; // num of states
String[] stateNames; // stateNames
int[] states; // state array
int[][] R; // reward lookup
double[][] Q; // Q learning
// actions
int[][] actions; // action mapping
// target
int target; // reach target to stop
@Override
public void init() {
// TODO Auto-generated method stub
}
// processing
@Override
public void process() {
// TODO Auto-generated method stub
/*
* 1. Set parameter , and environment reward matrix R
* 2. Initialize matrix Q as zero matrix
* 3. For each episode: Select random initial state Do while not
* reach goal state o Select one among all possible actions for the current
* state o Using this possible action, consider to go to the next state o Get
* maximum Q value of this next state based on all possible actions o Compute o
* Set the next state as the current state
*/
}
@Override
public double maxQ(int s) {
// TODO Auto-generated method stub
/* find out the max Q
*
*/
return 0;
}
@Override
public int policy(int state) {
// TODO Auto-generated method stub
/*
* base on the policy to goto state
* return goto state
*/
return 0;
}
@Override
public double Q(int s, int a) {
// TODO Auto-generated method stub
return Q[s][a];
}
@Override
public void setQ(int s, int a, double value) {
// TODO Auto-generated method stub
Q[s][a] = value;
}
@Override
public int R(int s, int a) {
// TODO Auto-generated method stub
return R[s][a];
}
@Override
public void printResult() {
// TODO Auto-generated method stub
/*
* Print the results
*/
}
@Override
public void showPolicy() {
// TODO Auto-generated method stub
// show each steps
}
}
3. Test the Q-Learning
You may base on this case:
// Sample Case: TO location C
// states A,B,C,D,E,F
// e.g. from A we can go to B or D
// from C we can only go to C
// C is goal state, reward 100 when B->C or F->C
// _______
// |A|B|C|
// |_____|
// |D|E|F|
// |_____|
// Sample output:
// Print result
// out from A: 0 90 0 72.9 0 0
// out from B: 81 0 100 0 81 0
// out from C: 0 0 0 0 0 0
// out from D: 81 0 0 0 81 0
// out from E: 0 90 0 72.9 0 90
// out from F: 0 0 100 0 81 0
//
// showPolicy
// from A goto B
// from B goto C
// from C goto C
// from D goto A
// from E goto B
// from F goto C
// Time: 0.023 sec.
What you should do :
- prepare the alpha, gamma, episodes, stateNames, states, statesCount, actions, target etc. (see previous step 2 code)
- instance the RL
- call these three functions.
process();
printResult();
showPolicy();
// sample code
public class TestCase {
public static void main(String[] args) {
// Sample Case: TO location C
// states A,B,C,D,E,F
// e.g. from A we can go to B or D
// from C we can only go to C
// C is goal state, reward 100 when B->C or F->C
// _______
// |A|B|C|
// |_____|
// |D|E|F|
// |_____|
// Sample output:
// Print result
// out from A: 0 90 0 72.9 0 0
// out from B: 81 0 100 0 81 0
// out from C: 0 0 0 0 0 0
// out from D: 81 0 0 0 81 0
// out from E: 0 90 0 72.9 0 90
// out from F: 0 0 100 0 81 0
//
// showPolicy
// from A goto B
// from B goto C
// from C goto C
// from D goto A
// from E goto B
// from F goto C
// Time: 0.023 sec.
// params
double alpha = 0.1;
double gamma = 0.9;
int episodes = 400;
// TODO
// PREPARE SOME OTHER PARAMS
long BEGIN = System.currentTimeMillis();
// Instance and call functions
// QLExample02 obj = new QLExample( alpha, gamma, episodes, stateNames,
// states, statesCount, actions, target);
// obj.process();
// obj.printResult();
// obj.showPolicy();
long END = System.currentTimeMillis();
System.out.println("Time: " + (END - BEGIN) / 1000.0 + " sec.");
}
}