Motivation

It’s easy to train a model against a particular dataset, but how does this model perform when introduced with new data? How do you know which machine learning model to use? Cross-validation answers these questions by assuring a model is producing accurate results and comparing those results against other models. Cross-validation goes beyond regular validation, the process of analyzing how a model does on its own training data, by evaluating how a model does on new data. Several different methods of cross-validation are discussed in the following sections:

Holdout Method

The holdout cross-validation method involves removing a certain portion of the training data and using it as test data. The model is first trained against the training set, then asked to predict output from the testing set. This is the simplest form of cross-validation techniques, and is useful if you have a large amount of data or need to implement validation quickly and easily.

Typically the holdout method involves splitting a dataset into 20-30% test data and the rest as training data. These numbers can vary - a larger percentage of test data will make your model more prone to errors as it has less training experience, while a smaller percentage of test data may give your model an unwanted bias towards the training data. This lack of training or bias can lead to Underfitting/Overfitting of our model.

K-Fold Cross Validation

K-Fold Cross Validation helps remove these biases from your model by repeating the holdout method on k subsets of your dataset. With K-Fold Cross Validation, a dataset is broken up into several unique folds of test and training data. The holdout method is performed using each combination of data, and the results are averaged to find a total error estimation.

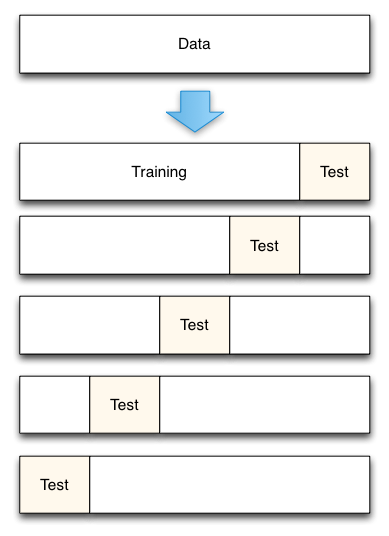
A “fold” here is a unique section of test data. For instance, if you have 100 data points and use 10 folds, each fold contains 10 test points. K-Fold Cross Validation is important because it allows you to use your complete dataset for both training and testing. It’s especially useful when evaluating a model using small or limited datasets.

Leave-P-Out / Leave-One-Out Cross Validation

Leave-P-Out Cross Validation (LPOCV) tests a model by using every possible combination of P test data points on a model. As a simple example, if you have 4 data points and use 2 test points, the model will be trained and tested as follows:

1: [ T T - - ] 2: [ T - T - ] 3: [ T - - T ] 4: [ - T T - ] 5: [ - T - T ] 6: [ - - T T ] 

Where “T” is a test point, and “-” is a training point. Below is another visualization of LPOCV:

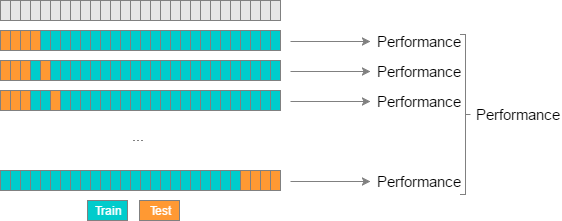
LPOCV can provide an extremely accurate error estimation, but can quickly become exhaustive for large datasets. The amount of testing iterations a model has to go through using LPOCV can be calculated using a mathematical combination n C P, with n being our total number of data points. We can see, for instance, that a LPOCV run using a dataset of 10 points with 3 test points would require 10 C 3 = 120 iterations.

Because of this, Leave-One-Out Cross Validation (LOOCV) is a commonly used cross-validation method. It is just a subset of LPOCV, with P being 1. This allows us to evaluate a model in the same number of steps as there are data points. LOOCV can also be seen as K-Fold Cross Validation, where the number of folds is equal to the number of data points.

Similar to K-Fold Cross Validation, LPOCV and LOOCV train a model using the full dataset. They are particularly useful when you’re working with a small dataset, but incur performance tradeoffs.

Conclusion

Cross-validation is a way to validate your model against new data. The most effective forms of cross-validation involve repeatedly testing a model against a dataset until every point or combination of points have been used to validate a model, though this comes with performance trade-offs. We discussed several methods of splitting a dataset for cross-validation:

• Holdout Method: Splitting a percent of data off as test data
• K-Fold Method: Dividing data into sections, using each as a test/train split
• Leave-P-Out Method: Using every combination of a number of points (P) as test data

Remarks

There are many different types of machine learning models, including Linear/Logistic Regression, K-Nearest-Neighbors, and Support Vector Machines - but how do we know which type of model is the best for our dataset? Using a model unsuitable for our data will lead to less accurate predictions, and could lead to financial, physical, or other forms of harm. Individuals and companies should make sure to cross-validate any models they put into use.

Code Examples

The provided code shows how to split a set of data with the three discussed methods of cross-validation using Scikit-Learn, a Python machine learning library.

holdout.py splits a set of sample diabetes data using the Holdout Method. In scikit-learn, this is done using a function called train_test_split() which randomly splits a set of data into two portions:

TRAIN_SPLIT = 0.7 ... dataset = datasets.load_diabetes() ... x_train, x_test, y_train, y_test = train_test_split(...) 

Note that you can change the portion of data used for training by changing the TRAIN_SPLIT value at the top. This should be a number from 0 to 1. Output from this file shows the number of training and test points used for the split. It may be beneficial to see the actual data points - if you would like to see these, uncomment the last two print statements in the script.

k-fold.py splits a set of data using the K-Fold Method. This is done by creating a KFold object initialized with the number of splits to use. Scikit-learn makes it easy to split data by calling KFold’s split() method:

NUM_SPLITS = 3 data = numpy.array([[1, 2], [3, 4], [5, 6], [7, 8], [9, 10], [11, 12]]) kfold = KFold(n_splits=NUM_SPLITS) split_data = kfold.split(data) 

The return value of this is an array of train and test points. Note that you can play with the number of splits by changing the associated value at the top of the script. This script not only outputs the train/test data, but also outputs a nice bar where where you can track the progress of the current fold:

[ T T - - - - ] Train: (2: [5 6]) (3: [7 8]) (4: [ 9 10]) (5: [11 12]) Test: (0: [1 2]) (1: [3 4]) ... 

leave-p-out.py splits a set of data using both the Leave-P-Out and Leave-One-Out Methods. This is done by creating LeavePOut/LeaveOneOut objects, the LPO initialized with the number of splits to use. Similar to KFold, the train-test data split is created with the split() method:

P_VAL = 2 data = numpy.array([[1, 2], [3, 4], [5, 6], [7, 8]]) loocv = LeaveOneOut() lpocv = LeavePOut(p=P_VAL) split_loocv = loocv.split(data) split_lpocv = lpocv.split(data) 

Note that you can change the P value at the top of the script to see how different values operate.

1. Holdout.py

2. k-fold.py

3. leave-p-out.py

References

1. https://towardsdatascience.com/cross-validation-in-machine-learning-72924a69872f
2. https://machinelearningmastery.com/k-fold-cross-validation/
3. https://www.quora.com/What-is-cross-validation-in-machine-learning
4. http://www.ebc.cat/2017/01/31/cross-validation-strategies/

Acknowledge: Python Machine Learning supervised by Amirsina Torfi, 2019.